Johannes Kepler, quando descobriu as leis do movimento elíptico dos planetas que hoje levam o seu nome, provavelmente já sabia da sua natureza revolucionária. A primeira vista, trocar órbitas circulares por órbitas elípticas pouco excêntricas poderia parecer um ligeiro aprimoramento nos detalhes de uma teoria bem-sucedida. Mas isto representava uma quebra fundamental do paradigma que afirmava ser o movimento dos corpos celestes perfeito (i.e., circular) e imutável, e intrinsecamente diferente dos imperfeitos e transientes movimentos na Terra. Mesmo após a sua contestação por Copérnico, o modelo Ptolomaico, com suas inúmeras categorias de movimentos circulares sobrepostos, era geralmente visto com entusiasmo, como a mais perfeita e precisa descrição do cosmos.
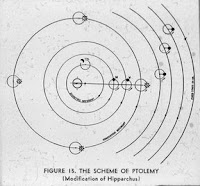Os cálculos feitos por Kepler com base nas observações de Tycho Brahe certamente excluíam um modelo geocêntrico com órbitas circulares, mas isso já era sabido a partir de observações muito mais imprecisas disponíveis já no período Helenístico. Muito mais importante foi a exclusão definitiva do modelo Ptolomaico. Mas isto não seria suficiente para excluir completamente qualquer modelo geocêntrico. Quaisquer que fossem as observações, seria sempre possível acrescentar mais epicíclos no modelo de Ptolomeu, até que este se encaixasse novamente nas observações, dentro da precisão observacional da época. De fato, foi exatamente desta forma que este modelo se desenvolvera.
Mas Kepler foi além. Seus cálculos permitiam excluir não só o modelo de Ptolomeu, mas também o modelo misto de Brahe (onde os planetas orbitam o Sol, que orbita a Terra), e até o modelo helicentrico com órbitas circulares de Copérnico. Depois de muita hesitação e dúvida, Kepler descobriu que um modelo heliocêntrico com órbitas elípticas se encaixava muito bem às observações.
A esta altura, como ele poderia determinar qual a melhor teoria? As observações eram compatíveis com dois modelos distintos: Um
modelo heliocêntrico com órbitas elípticas, e um modelo geocêntrico com epicíclos adicionais. Qual deles era o `melhor'? Se partíssemos da hipótese segundo a qual os movimentos celestes devem ser sempre composições de movimentos circulares, aceita quase axiomaticamente pelos estudiosos desde a época helenística, então teríamos que concluir que Kepler e Brahe, longe de provar o heliocentrismo, o refutaram, pelo menos na sua forma mais simples (lembrando que a simplicidade era um dos grandes atrativos da teoria de Copérnico).
Kepler, porém, ao se ater à hipótese heliocêntrica, encontrou mais do que simplesmente órbitas elípticas. Existiam duas outras leis, relacionando o tamanho, velocidade e período das órbitas, que se aplicavam ao movimento de todos os planetas. Os raios e períodos dos vários ciclos e epicíclos ptolomaicos eram essencialmente arbitrários, escolhidos a posteriori para se ajustarem às observações. O novo modelo de Kepler tinha a vantagem de
unificar um grande conjunto de observações por meio de algumas poucas leis fenomenológicas simples e elegantes. Uma explicação
mais fundamental para estas leis de não tardou a vir. Inspirado diretamente por Kepler (e Galileu), Isaac Newton lançou os alicerces da física moderna com sua teoria da gravidade universal, que se aplicava igualmente ao céu e à Terra. As esferas de cristal e os epicíclos subitamente se tornaram tão anacrônicos como descrição do universo quanto os proverbiais elefantes nas costas de uma tartaruga. Nada mal para a conseqüência de um ligeiro aprimoramento nos detalhes de uma teoria bem-sucedida.
A digressão acima ilustra um ponto recorrente na história da cosmologia. Em quase todas as épocas desde os primórdios das ciências naturais na Grécia antiga, os estudiosos dispunham de um modelo que explicava adequadamente quase todas as observações disponíveis. Acreditavam portanto dispor de uma descrição razoavelmente precisa e completa para o universo. Pequenas discrepâncias não eram (ou são) ignoradas de todo, mas em vista do sucesso da teoria geralmente aceita, era razoável supor que aquelas desapareceriam após ligeiras correções. As grandes revoluções no entendimento do cosmo neste período tiveram origem em tentativas de explicar tais discrepâncias por meio da ruptura com um ou mais fundamentos do paradigma aceito (muitas vezes de forma implícita) até então. Foi assim quando Kepler prescindiu de órbitas círculares, ou quando Newton formulou explicitamente leis de aplicação universal acima e abaixo da 'esfera lunar', ou também quando Einstein modificou a extraordinariamente bem-sucedida dinâmica newtoniana com base em um novo conjunto de postulados, e ainda quando Hubble mostrou que o universo não era estático.
Nas últimas décadas, a cosmologia baseada na hipótese de um Big Bang quente com sua dinâmica dada pela teoria da relatividade geral tem sido extremamente bem-sucedida em explicar precisamente uma grande quantidade de observações, que vão desde a abundância relativa de elementos leves até a estrutura em grandes escalas do universo atual, passando pela natureza térmica e as anisotropias da radiação cósmica de fundo. O recente surgimento da chamada cosmologia de precisão só fez confirmar os fundamentos deste modelo, com uma acuidade sem precedentes. Mas ainda há alguns pontos desconhecidos, e ligeiras discrepâncias entre teoria e observações. Por exemplo, aparentemente existem pequenos desvios na gaussianidade e anisotropia estatística da radiação cósmica de fundo. E não sabemos exatamente do que consistem as chamadas matéria e energia escuras, ou a origem do campo escalar que supostamente gerou a inflação. Ou qual é exatamente a topologia do universo. Talvez estes problemas tenham soluções relativamente simples dentro do paradigma vigente. Mas é também possível que sejam indícios de uma nova física, e/ou de um entendimento qualitativamente mais profundo do cosmo.
PS: Agradecimentos especiais ao Bernardo.
PS2: Veja a parte II aqui
Continue lendo...>>
<< Pronto!
Eu já estudei ou visitei alguns departamentos acadêmicos excelentes. Encontrei pesquisa de qualidade, bons professores, equipamentos de ponta, localizações paradisíacas. Mas em termos de pura classe, nenhum supera a física da UFMG. Sexta passada fui ver um seminário (pré-defesa) da Mariana Malard. E foi com grata surpresa que me deparei não só com uma palestra sobre os modelos de Heisenberg e sigma não-linear, mas também com um verdadeiro convescote ocorrendo em paralelo dentro da sala de seminários. Entre um gole e outro de cerveja, os presentes faziam comentários pertinentes, enquanto circulavam biscoitos e salgadinhos.
Depois da comida, uma pausa para a digestão
Mortos e feridos II
O famoso monte Mauna Homer. No momento da foto, já se ouviam os ruídos do fluxo piroclástico
Não tiramos fotos da comida, mas a cozinha parecia Nova Orleans pós-Katrina
Enquanto meditávamos na sala, a Mari deu um jeito na cozinha
